在上學期教series時,講起1 + 2 + 3 + 4 + …的結果是無限時,我等待著學生說一聲反對。可惜,沒有學生問我為何不是-1/12。
我只好自討沒趣地說出如果以其他方法定義的話,如計出 Grandi's series 1-1+1-1+1-... =1/2。當然講下去,就說起"黎曼猜想"Riemann Hypothesis (RH)。讀數的不知RH,那就如同登山愛好者不知珠穆朗瑪峰。
說RH,我就想起我之前談過的漫畫《神通小偵探》23集其中一個故事《另一個世界》。
 |
| 神通小偵探 23集 封面關於RH的部份 |
故事內容:宣告快完成黎曼猜想證明的數學家Kenneth Refla卻突然消失了。他在家中留下了四行詩、並在4位熟人處分別留下了一幅畫。4張畫中隱藏的真實是……?
要了解故事,要先了解什麼是RH。我以故事中最簡單的解釋開始說起:
RH就是有一百萬美元獎金的問題。現在有興趣知什麼是RH了吧!那聽聽燈馬的正常說明:
簡單來說,RH就是證明Riemann Zeta function ζ(s) = 0 的所有複數解的實數部份都是1/2。
什麼是Riemann Zeta function?就是
這series在s大於1 的實數時,我們直接可計算出數目。我們可用complex analysis中的Analytic continuation (解析延拓)把這function定義到整個複數空間。如以這定義下,我們可得出一些奇怪(不配合直觀)但合理(配合定義,不有矛盾)的結果:
這就是我一開頭說的1+2+3+4+...為何是-1/12。
最後說回《神通小偵探》,那個想完成黎曼猜想證明的數學家Kenneth Refla最後如何?
先看他留下的四幅畫:

再配合他留下的四行詩:
I left for the journey to the unknown world.
I pulled down the dragon and finished him at the infinite land.
I'd rather choose death at the most infinite land as I know.
I as a king saw that all the rest has come to naught.
你可能會猜,這數學家就好像其他嘗試證明黎曼猜想的人一樣沒有成功。是的,燈馬最後找到的是這數學家的墓:

真相真的是這麼絕望?想知道可看這漫畫,也可在詩中和這墓碑中找出重要的線索。
----------------------------------------------
事實上,這偵探故事的推理成份不算高,但故事中的數學解釋十分豐富,數學愛好者可一看。









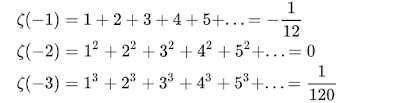




留言
發佈留言